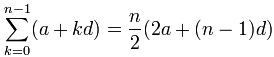Sequence
A Sequence is a set of things (usually numbers) that are in order.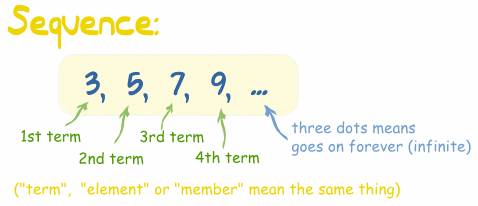
Arithmetic Sequence
In an Arithmetic Sequence the difference between one term and the next is a constant.In other words, we just add the same value each time ... infinitely.
Example:
| 1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
This sequence has a difference of 3 between each number.
{a, a+d, a+2d, a+3d, ... }
where:- a is the first term, and
- d is the difference between the terms (called the "common difference")
Example: (continued)
| 1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
- a = 1 (the first term)
- d = 3 (the "common difference" between terms)
{a, a+d, a+2d, a+3d, ... }
{1, 1+3, 1+2×3, 1+3×3, ... }
{1, 4, 7, 10, ... }
Rule
We can write an Arithmetic Sequence as a rule:
xn = a + d(n-1)
(We use "n-1" because d is not used in the 1st term).
Example: Write the Rule, and calculate the 4th term for
| 3, 8, 13, 18, 23, 28, 33, 38, ... |
This sequence has a difference of 5 between each number.
The values of a and d are:- a = 3 (the first term)
- d = 5 (the "common difference")
xn = a + d(n-1)
= 3 + 5(n-1)
= 3 + 5n - 5
= 5n - 2
So, the 4th term is:
x4 = 5×4 - 2 = 18
Is that right? Check for yourself!
Arithmetic Sequences are sometimes called Arithmetic Progressions (A.P.’s)
Summing an Arithmetic Series
To sum up the terms of this arithmetic sequence:
a + (a+d) + (a+2d) + (a+3d) + ...
use this formula: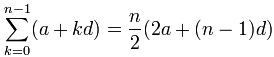
What is that funny symbol? It is called Sigma Notation
And below and above it are shown the starting and ending values:
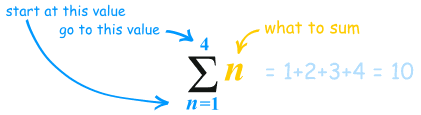
Here is how to use it:| (called Sigma) means "sum up" |
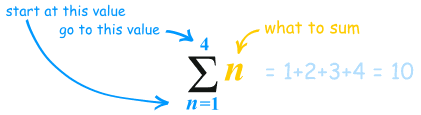
It says "Sum up n where n goes from 1 to 4. Answer=10
Example: Add up the first 10 terms of the arithmetic sequence:
{ 1, 4, 7, 10, 13, ... }
The values of a, d and n are:- a = 1 (the first term)
- d = 3 (the "common difference" between terms)
- n = 10 (how many terms to add up)
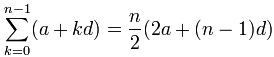
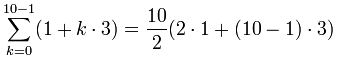
= 5(2+9·3) = 5(29) = 145
Check: why don't you add up the terms yourself, and see if it comes to 145
Why Does the Formula Work?
Let's see why the formula works, because we get to use an interesting "trick" which is worth knowing.First, we will call the whole sum "S":
S = a + (a + d) + ... + (a + (n-2)d) + (a + (n-1)d)
Next, rewrite S in reverse order:
S = (a + (n-1)d) + (a + (n-2)d) + ... + (a + d) + a
Now add those two, term by term:| S | = | a | + | (a+d) | + | ... | + | (a + (n-2)d) | + | (a + (n-1)d) |
| S | = | (a + (n-1)d) | + | (a + (n-2)d) | + | ... | + | (a + d) | + | a |
| 2S | = | (2a + (n-1)d) | + | (2a + (n-1)d) | + | ... | + | (2a + (n-1)d) | + | (2a + (n-1)d) |
Each term is the same! And there are "n" of them so ...
2S = n × (2a + (n-1)d)
Now, just divide by 2 and we get:
S = (n/2) × (2a + (n-1)d)